Understanding image sharpness part 1A:
Resolution and MTF curves in film and lenses
by Norman Koren
 |
|
In
this page we illustrate how MTF is used to characterize the
performance of film and lenses.
| Green is for geeks. Do you get excited by a good equation? Were you passionate about your college math classes? Then you're probably a math geek-- a member of a maligned and misunderstood but highly elite fellowship. The text in green is for you. If you're normal or mathematically challenged, you may skip these sections. You'll never know what you missed. |
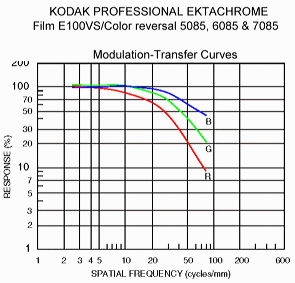 | The
curve on the left is the MTF for Kodak
E100VS reversal (slide) film (similar to Elite Chrome 100). A
different
MTF is shown for each color layer: red, green, and blue (R, G, and B).
Green is the most important because the eye is far more
sensitive to it than to other colors. The green curve is close
to the MTF curve for Fujichrome
Provia 100F.
Most film MTF curves can be closely approximated by a function known as the Lorentzian, MTFfilm( f ) = 1/(1+( f/f50)2)f is frequency; f50 is the frequency where MTF = 0.5 = 50%. For the E100VS green layer, f50 = 40 line pairs/mm. For the mathematically challenged, MTF( f ) is expressed in functional notation, which indicates that MTF is a function of frequency, f. |
Electrical engineers will note that this curve has a second order Butterworth response. Second order means that at high frequencies, f >> f50, response drops twice as fast as frequency increases; it is proportional to 1/ f 2. This is also called this a 12 dB (decibels) per octave rolloff (6 dB per octave per order).The MTFcurve program illustrates the effects of MTF on the input target. MTF is applied only in the horizontal direction (it's two dimensional in actual images). The blue curve below the target is the film MTF, expressed in percentage-- the scale on the left applies. It closely approximates the green curve for Ektachrome E100VS. The red curve shows the density of the bar pattern. The 50% and 10% amplitudes are 40 line pairs/mm, as expected, and 120 line pairs/mm. This plot is
generated from Matlab by entering
|
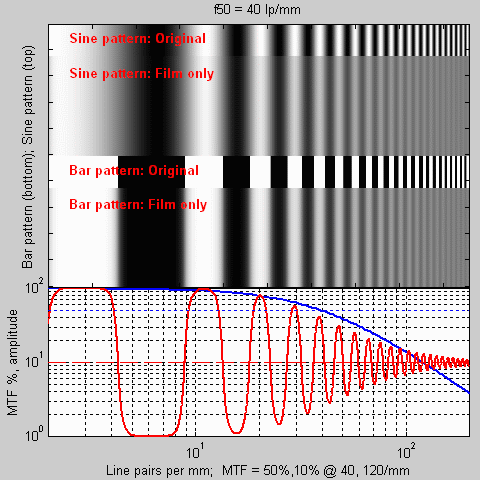 |
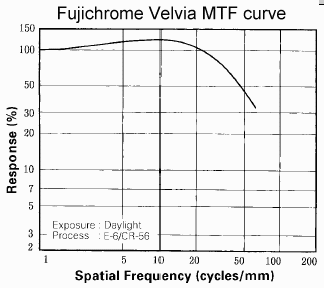 | The MTF curve on the left
is from an old data sheet for Fujichrome Velvia,
a highly saturated ASA 50 slide film known for its sharpness. Something
is different here: a boost in the MTF response, which peaks at around
125%
at 10 line pairs/mm. What can this mean?
From my former career, I recognized this curve as characteristic of pulse slimming equalizers, widely used in older magnetic disk drives to sharpen readback pulses so more data can be squeezed into a given area. By adding one more parameter, fboost, I was able to fit it reasonably well. MTFfilm( f ) = k / (1+(( f - fboost) / f50a )2)fboost is the frequency of maximum MTF. The percentage boost depends on the ratio, fboost / f50. fboost must be less than f50 /2. k is a constant set so that MTF(0) = 1. One caution about this equation: it rolls off more rapidly at high spatial frequencies ( f >> f50) than the equation without fboost (or fboost = 0). This boost is called the adjacency effect boost for reasons described below. It is similar in nature to the boost caused by digital sharpening. |
f50a = sqrt( f502-2 f50 fboost - fboost2) so that f50 (as entered in MTFcurve) is still the 50% MTF frequency.
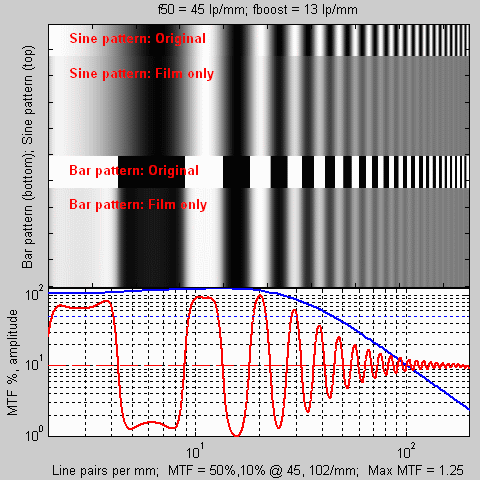
The striking feature of the response, shown in the red curve below the image, is the exaggerated contrast boundaries. Tones overshoot their low frequency (steady state) levels, and the result is plainly visible. The overall effect is that this image appears slightly sharper than the image above for Ektachrome E100VS or Fuji Provia 100F, even though it has slightly lower response at 100 line pairs/mm.
This effect is similar to the sharpen or unsharp mask functions in image editing programs.
There is a fairly elementary explanation of how this happens in film. It it particularly noticeable with black & white films developed in highly diluted (one-shot) developers. Visualize a contrast boundary between two areas, one side of which is heavily exposed (a highlight) and the other lightly exposed (a shadow). As the film is developed (particularly in the interval between between agitations), the developer in the heavily exposed area becomes depleted more rapidly than the developer in the lightly exposed area, slowing down the development. Some of the developer diffuses across the boundary, so that the developer in the heavily exposed area adjacent to the boundary is less depleted than in the rest of the region, hence develops more rapidly, and the developer in the lightly exposed area adjacent to the boundary is more depleted, hence develops more slowly. The result is an exaggerated contrast boundary, as illustrated above. This is known as the adjacency effect, and film/developer combinations that exhibit it are said to have high acutance. In Velvia, the diffusion probably takes place inside the film.
The adjacency effect increases the perceived image sharpness,
though it can become irritatingly obvious if it's overdone. It boosts
the
the MTF 50% frequency, but it has relatively little effect on the 10%
level,
which is related to perceived line pairs per mm resolution.
Developing
technique affects MTF, particularly for B&W films, where there
is a
large choice of developers and agitation procedures. Development
options
are more limited for color films.
|
Take this data with a grain of salt. I have limited evidence that color negatives are actually sharper. Andreas Kaseder published a small comparison of ASA 100 films (part of his Nikon 4000 ED review) that seems to indicate that negative film is sharper but grainier. I've made amazingly sharp prints of the Aspens on the Pitkin Creek trail, taken with Kodacolor Gold 100. The likely reason that slide film has poorer sharpness is that
it's
made to be displayed directly. Dark tones must be deep and rich; Dmax
is
much higher than for negative films, hence more dye is needed. Emultion
layers may have to be thicker to accomodate this.
|
Kodak publishes MTF data for some color reversal and B&W negative films. Go to Kodak Professional Products or Kodak Consumer Products- Film and navigate from there. Searching for MTF on Kodak's main page also works well. Kodak Germany publishes MTF curves for Gold films, called Farbwelt in German. Ektachrome E200 has f50 = 34 lp/mm. Kodak T-MAX 100 has f50 = 125 lp/mm and T-MAX 400 has f50 = 100 lp/mm with 20% boost. T-MAX P3200 has f50 = 85 lp/mm. These MTF's are quite striking-- far beyond any color reversal film! Photodo's page on 35 mm, medium format, or large format? indicates that T-MAX 100 is indeed a remarkable film. 35 mm T-MAX 100 outperformed medium format Tri-X using very fine equipment. Photodo's articles are worthy of serious study. Kodak also uses a measurement called print grain index for prints.
Fujifilm publishes MTF data for all their films. Go to Consumer Film Product Line-up or Professional Film Product Line-up and navigate from there. Fujicolor NHGII ASA 800 and NPH 400 color negative films have f50 = 45 lp/mm.
There is one troubling aspect to some manufacturer's
MTF curves, for
example Fujichrome
Provia 100F. MTF should be 100% at very low frequencies, but
it remains
flat at 120% from 10 lp/mm down to 1 lp/mm. There are three possible
reasons.
(1) The adjacency effect extends to extremely low spatial frequencies.
Doubtful. 1 lp/mm is awfully low. (2) The graphic arts department took
liberties with the plot before sending it out for publication. This
happened
to me in the old days before I had access to computer tools. (3) The
marketing
department cheated. It happens.
| The Imatest program allows you to measure the MTF of digital cameras or digitized film images. You can't measure an individual component in isolation, but you can compare components, such as lenses, with great accuracy. Imatest also measurs other factors that contribute to image quality. |
 MTF
for film is rather simple-- it's the same in all directions and uniform
throughout the film surface. Not so lenses. MTF is a function of the
distance
from the image center, the aperture (f-stop), the spectrum of the
light, the focal length (for zooms), and even
the focusing distance (macro lenses are designed to maintain good MTF
at
close focus). Not only that, but there are two
MTF's at each point:
one along the radial (or sagittal) direction (pointing away from the
image
center) and one in the tangential direction (along a circle around the
image center), at right angles to the radial direction. Because of
this,
the MTF curve cannot be displayed in the same way as for film.
MTF
for film is rather simple-- it's the same in all directions and uniform
throughout the film surface. Not so lenses. MTF is a function of the
distance
from the image center, the aperture (f-stop), the spectrum of the
light, the focal length (for zooms), and even
the focusing distance (macro lenses are designed to maintain good MTF
at
close focus). Not only that, but there are two
MTF's at each point:
one along the radial (or sagittal) direction (pointing away from the
image
center) and one in the tangential direction (along a circle around the
image center), at right angles to the radial direction. Because of
this,
the MTF curve cannot be displayed in the same way as for film.
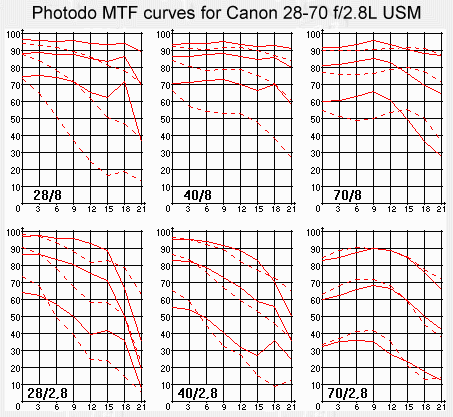
The MTF curves on the right are from the Photodo (old site) test of the Canon 28-70mm f/2.8L lens. Photodo is an outstanding Internet lens test resource, with 458 lenses optically MTF tested as of June 2000. Photodo curently uses Imatest for its lens tests. In their page, Understanding the MTF graphs, numbers and grades, they state,
"The graphs show MTF in percent for the three line frequencies of 10 lp/mm, 20 lp/mm and 40 lp/mm, from the center of the image (shown at left) all the way to the corner (shown at right). The top two lines represent 10 lp/mm, the middle two lines 20 lp/mm and the bottom two lines 40 lp/mm. The solid lines represent sagittal MTF (lp/mm aligned like the spokes in a wheel). The broken lines represent tangential MTF (lp/mm arranged like the rim of a wheel, at right angles to sagittal lines). On the scale at the bottom 0 represents the center of the image (on axis), 3 represents 3 mm from the center, and 21 represents 21 mm from the center, or the very corner of a 35 mm film image. Separate graphs show results at f8 and full aperture. For zoom lenses, there are graphs for each measured focal length."
They state elsewhere that performance at 10 line
pairs/mm is indicative of
the lens contrast while 40 line pairs/mm is indicative of its sharpness.
Lens performance is typically limited by aberrations
at large apertures and diffraction
at small apertures. Aberrations depend on lens design and manufacturing
quality; they differ markedly for different lenses. Diffraction is a
fundamental physical effect; it depends on the aperture alone. A lens
is sharpest between the two extremes, near its optimim
aperture,
which tends to be around f/8 or f/11 for the 35mm format. It is smaller
(as low as f/4) for compact digital cameras and larger (f/11 to f/22)
for large format cameras.
Unlike film, the MTF of lenses don't necessarily match the second order 1/(1+( f / f50)2) equation. MTF rolloff can vary widely, depending on lens design and manufacturing tolerance. To accommodate this, MTFcurve has an input variable for the order of the lens's MTF rolloff, lord, which defaults to 2 if not entered or if entered as 0. The lens MTF equation becomes,
MTFlens(f) = 1/(1+|f/flens|lord) (lord defaults to 2 in MTFcurve if not entered)Flens is the frequency where lens MTF = 0.5 = 50%, corresponding to f50 in film. We use lord = 2, which appears to be an adequate approximation for typical lenses, until better information is available. It's not easy to derive lord from Photodo's data because most of the curves are above MTF = 50%; you need to look at MTF below 30% to get a clear picture of the rolloff. Flens can be estimated by interpolating between curves if MTF at 40 line pairs/mm (MTF40) is below 50%. Or it can be estimated from MTF40 using the following table, which is based on the inverse of the second order equation, flens = 40/sqrt(1/MTF40-1), where MTF40 is expressed as a fraction rather than a percentage. Sqrt can be replaced by exponentiation to the 1/lord power ( flens = 40/(1/MTF40-1)^(1/lord) ) when lord is not 2.
| MTF40 | 20% | 30% | 40% | 50% | 60% | 70% | 80% |
| flens (1/mm) | 20 | 26.2 | 32.6 | 40 | 49 | 61 | 80 |
| The
Canon
28-70mm f/2.8L lens in this test is an outstanding performer,
achieving
a Photodo
rating
of 3.9 out of a possible 5, about as good as zoom lenses for the 35mm
format (covering 43mm diagonal) get. At 40mm,
f/8, it's as sharp as a first rate prime (single focal length) lens.
With
MTF40 around 70% at f/8, flens is around 61 line
pairs/mm The down
side: it's expensive (over $1000 US), large, and heavy. But sharp. The
photo.net
review is full of hypebole like, "one *bleeping* sharp
zoom!," "sharpness
and contrast is spectacular," "a stunning piece of glass," etc. Since
35mm lenses don't get much better I use this lens as the standard for
the
"excellent 35mm lens" for the remainder of this article.
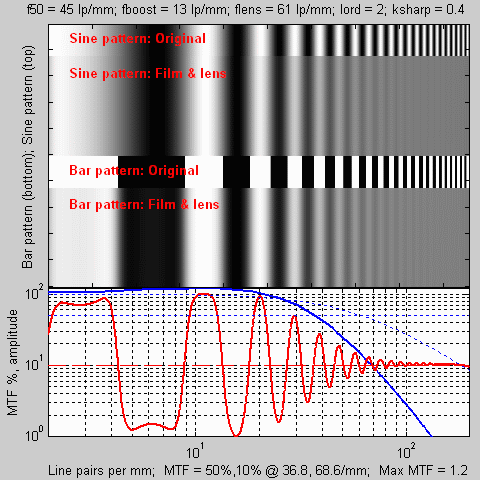
The plot on the right, generated by MTFcurve2 45 13 61 shows the combined response of Velvia film and the excellent 35mm lens. The red curve is the spatial response, the blue curve is the combined MTF, and the thin blue dashed curve is the MTF of the lens only. The 50% and 10% points for MTF are now 36.8 and 68.6 line pairs/mm. This is the best that can be expected for an excellent lens covering 43mm diagonal, optimum aperture, correct focus, sturdy camera support, and good atmospheric conditions. |
 |
| David Jacobson's Lens Tutorial A excellent short text on lenses with a fine description of factors that affect resolution and MTF. Fairly technical. |
| Paul van Walree has an excellent description of lens aberrations. |
| Lens aberrations A mathematical description of the Seidel aberrations from James R. Graham, U.C. Berkeley Professor of Astronomy. |
| Photodo.com (old) | Photodo.com (new) A great source of MTF tests for 35mm lenses. Optical MTF tests on the old site were discontinued in 2000, but the current incarnation of Photodo uses Imatest for its lens tests. |
| Schneider Optics has a page on Quality criteria of lenses that includes an explanation of MTF. If you read this page carefully, you'll find a minor error in their MTF diagram. They also publish MTF data for their large format and enlarging lenses. The curves look like Photodo's except that they're done at 5, 10, and 20 line pairs per mm instead of 10, 20, and 40. I suppose this is more appropriate for large format. Unfortunately these curves are based on computer simulation rather than real measurements, which will always be a little worse. Their arch competitor Zeiss has unkind things to say about this technique. |
| http://www.page.sannet.ne.jp/tsoka/rollei6000/index_e.html has MTF curves for Rollei medium format lenses-- similar to lenses used by Hasselblad. |
| Canon has MTF data its for EOS lenses, measured at 30 and 10 lp/mm. It's evidently calculated rather than measured; it tends to be a bit more optimistic than Photodo.com. Compare, for example, the 28-70mm f/2.8L. Similar data is available on a French language site. |
| Leica has published MTF data for several of its outstanding M-System (rangefinder) and R-System (SLR) lenses as PDF Product information, linked on the lower right of these two pages. MTF data is for 5, 10, 20, and 40 lp/mm. They state that the 5 and 10 lp/mm data relates to large object contrast while the 20 and 40 lp/mm data relates to small object resolution. It's instructive to compare Leica's data with detailed lens performance observations by Erwin Puts. |
| Robert Monaghan's Lens Resolution Testing page contains some serious discussion about image sharpness issues and links to test targets. |
Diffraction worsens as the lens is stopped down (the f-stop is increased). The equation for the Rayleigh diffraction limit, adapted from R. N. Clark's scanner detail page, is,
Rayleigh limit (line pairs per mm) = 1/(1.22 Nω)N is the f-stop setting and ω = the wavelength of light in mm = 0.0005 mm for a typical daylight spectrum. (0.00055 mm is the wavelength of green light, where the eye is most sensitive, but 0.0005 mm may be more representative of daylight situations.) I've seen a simple rule of thumb, Rayleigh limit = 1600/N, which corresponds to ω = 0.000512 mm. The light circle formed by diffraction, known as the Airy disk, has a radius equal to1/(Rayleigh limit).
The MTF at the Rayleigh limit is about 9%. Significant Rayleigh limits are 149 lp/mm @ f/11, 102 lp/mm @ f/16, 74 lp/mm @ f/22, and 51 lp/mm @ f/32. Larry, an experienced lens designer, finds these numbers to be somewhat conservative because the Rayleigh limit is based on a spot, which has lower resolution than a band. His numbers of 125 lp/mm @ f/16 and 64 lp/mm @ f/32 are derived from a Kodak chart he contributed to Robert Monaghan's Lens Resolution Testing page. Most lenses are aberration-limited (relatively unaffected by diffraction) at f/8 and below. The OTF (optical transfer function) curve in David Jacobson's Lens Tutorial shows how MTF (the magnitude of OTF) varies with spatial frequency for a purely diffraction-limited lens at f/22.
We can derive some interesting relationships from David Jacobson's graph. At the Rayleigh diffraction limit of 68 lp/mm (for f/22, ω = 555 nm = 0.000555 mm), MTF is approximately 9%. It is 10% at about 64 lp/mm and 50% at 32 lp/mm. The following relationships therefore hold for diffraction-limited lenses:
f10 = 0.77/(Nω) ; N = F-stop; ω = the wavelength of light in mm = 0.0005mmThe diffraction curve is somewhat difficult to express mathematically, but it can be approximated-- matched at the 10% and 50% MTF points-- by the equation used in the MTFcurve program ( f50 is the same as flens; f50 and lord are the third and fourth input arguments to MTFcurve),
f50 = 0.38/(Nω) = 0.46*Rayleigh limit
MTFdiffraction-ltd(f) ~= 1/(1+| f/f50|lord) ( f50 = 0.38/(Nω); lord = 3.17)The question remains, at what f-stop does a lens become diffraction limited? The best estimate is the f-stop where the diffraction-limited f50 (0.38/(N ω)) equals flens-- the 50% MTF frequency at the sharpest aperture. For the excellent 35mm lens, flens = 61 lp/mm. The f-stop with the same diffraction-limited f50 is N = 0.38/(61*0.0005) = 12.5. We can therefore say with some confidence that good 35mm lenses are relatively unaffected by diffraction at f/8 and below, moderately affected at f/11, and diffraction-limited at f/16 and beyond. Such lenses should only be stopped down beyond f/11 (larger f-stops for larger formats) when extreme depth of field is required. Diffraction in digital cameras is discussed here.
| The Imatest program allows you to measure the MTF of digital cameras or digitized film images. You can't measure an individual component in isolation, but you can compare components, such as lenses, with great accuracy. Imatest also measurs other factors that contribute to image quality. |
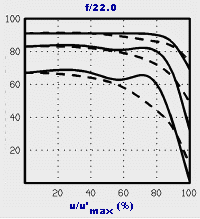 Thanks
to Schneider's large
format lens data, we can compare large format image quality
to 35mm.
The MTF curve on the left is for the 150mm f/5.6 Schneider Apo-Symmar
lens,
focused at infinity at f/22. It could be a little better than actual
lens
performance because it's derived from computer simulation. But it's
almost
certainly worse than optimum because the lens is diffraction-limited at
f/22; it is almost certainly sharper at f/11 and f/16. Its image circle
is u' = 110mm, more than sufficient to cover the 4x5
(inch) format with room for camera movements. The principal difference
between this curve and the Photodo curves (above) is that the three
lines
(top to bottom) represent 5, 10, and 20 lines per mm (instead of 10,
20,
and 40). This is a first class view camera lens; hence we'll refer to
it
as an "excellent 4x5
lens."
Thanks
to Schneider's large
format lens data, we can compare large format image quality
to 35mm.
The MTF curve on the left is for the 150mm f/5.6 Schneider Apo-Symmar
lens,
focused at infinity at f/22. It could be a little better than actual
lens
performance because it's derived from computer simulation. But it's
almost
certainly worse than optimum because the lens is diffraction-limited at
f/22; it is almost certainly sharper at f/11 and f/16. Its image circle
is u' = 110mm, more than sufficient to cover the 4x5
(inch) format with room for camera movements. The principal difference
between this curve and the Photodo curves (above) is that the three
lines
(top to bottom) represent 5, 10, and 20 lines per mm (instead of 10,
20,
and 40). This is a first class view camera lens; hence we'll refer to
it
as an "excellent 4x5
lens."
We can find the lens's 50% MTF value, flens, by modifying the above equation to flens = 20/sqrt(1/MTF20-1), or we can also use the above table by substituting MTF20 for MTF40 and dividing flens by 2. Since MTF20 ~= 66%, we estimate flens to be 28 line pairs per mm. This is just under half the value for the excellent 35mm lens and just slightly under the diffraction limit ( f50 = 32 lp/mm for f/22). Even at optimum aperture (around f/11) a view camera lens is not likely to be as sharp as the excellent 35mm lens; it has to cover about 4 times the image circle (16 times the area). Next we run MTFcurve 45 13 28, (Velvia film + lens) and we find that the 50% and 10% MTF values of the film + lens are 27.1 and 49.9 line pairs/mm. Sharpness is almost entirely limited by the lens; the film hardly plays a role.
Assuming a 35mm frame is cropped for an 8x10 print, a 4x5 frame is 4 times larger. The ratio of total detail at the 50% level is 4*27.1/36.8 = 2.94. The ratio at the 10% level is 4*49.9/68.6 = 2.91. A 4x5 image can therefore resolve approximately three times the linear detail of 35mm, assuming both employ good technique: excellent lenses and film, optimum aperture, correct focus, sturdy camera support, good atmospheric conditions, etc. Since the passing of the Speed Graphic era, such good technique has been standard practice in large format photography; it's less common with 35mm. A 24x30 inch print from 4x5 would have the same detail as an 8x10 from 35mm. It can be extremely sharp! This result is in substantial agreement with R. N. Clark's scanner detail page. If we are to believe Kodak's T-MAX 100 data, the ratio would be lower: 35mm images would be phenomenally sharp, limited only by the lens.
If you are interested in large format photography, Large Format Photography . Info, edited by Quang-Tuan Luong and Bjorn Nilsson, is an outstanding resource.
Back to Part
1: Introduction
| Next: Part 2: Scanners and
sharpening

| Images and text copyright © 2000-2013 by Norman Koren. Norman Koren lives in Boulder, Colorado, where he worked in developing magnetic recording technology for high capacity data storage systems until 2001. Since 2003 most of his time has been devoted to the development of Imatest. He has been involved with photography since 1964. |  |